Hybrid particle-mesh methods for simulating free-surface waves
The wealth of different numerical methods developed in the Computational Fluid Dynamics (CFD) community over the past decades can roughly be categorized in two different classes. At the one side are the Eulerian mesh-based method, solving the governing flow equations at a fixed mesh. At the other side are the Lagrangian particle-based method, in which material volumes are tracked by means of a set of moving particles.
Hybrid particle-mesh methods attempt to combine the advantages of the Eulerian methods (fast and efficient solvers) with the flexibility offered by Lagrangian methods (following material interfaces and advection of material quantities). As such, the potential of hybrid particle-mesh approaches has been recognized in various engineering fields and in the graphics community for the physics based animation of fluid flows.
However, various issues are to date persistent to the particle-mesh methods. Most importantly, a generic framework (being both physically and mathematically correct and numerically accurate) for the interaction between the Lagrangian particles and the Eulerian mesh is still missing. This gap in the fundamental understanding of the hybrid particle-mesh methods leads to ad hoc model fixes in the state-of-the-art particle-mesh methods.
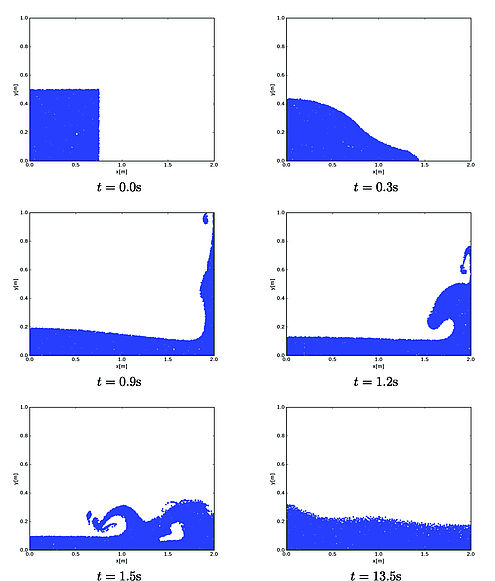
In this PhD study, the fundamentals of the particle-mesh methods are studied and improved, where the specific application in mind is the simulation of free surface waves in a Numerical Wave Tank. Starting point is to derive, implement and assess a model formulation for single phase, advection dominated flow problems after which the extension is made to derive a model formulation for multi-phase flows involving large jumps in material properties (i.e. air-water density ratio).
Contact
Ir. J.M. Maljaars PhD-student
Dr.ir. R.J. Labeur Supervisor
Prof.dr.ir. W.S.J. Uijttewaal Promotor